Дисконтированная стоимость (PV) — что это. Формула и пример расчета в Excel
Оба понятия из заголовка этого раздела, дисконтированная (приведенная) стоимость, ПС (presentvalue, или PV), и чистая дисконтированная (приведенная) стоимость, ЧПС (netpresentvalue, или NPV), обозначают текущую стоимость ожидаемых в будущем денежных поступлений.
В качестве примера рассмотрим оценку инвестиции, обещающей доход 100 долл. в год в конце нынешнего и еще четырех следующих лет. Предполагаем, что эта серия из пяти платежей по 100 долл. каждый гарантирована и деньги непременно поступят. Если бы банк платил нам годовой процент в размере 10% при депозите на пять лет, то эти десять процентов как раз и составляли бы альтернативную стоимость инвестиции — эталонную норму прибыли, с которой мы сравнивали бы выгоду от нашего вложения.
Можно вычислить ценность инвестиции путем дисконтирования денежных поступлений от нее с использованием альтернативной стоимости в качестве ставки дисконтирования.
Формула расчета в Excel дисконтированной (приведенной) стоимости (PV) = ЧПС(C1;B5:B9)
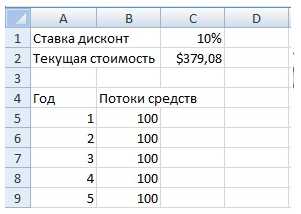
Приведенная стоимость (ПС) в объеме 379,08 долл. и есть текущая стоимость инвестиции.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
Предположим, что данная инвестиция продавалась бы за 400 долл. Очевидно, она не стоила бы запрашиваемой цены, поскольку — при условии альтернативного дохода (учетной ставки) в размере 10% — реальная стоимость этого капиталовложения составляла бы только 379,08 долл. Здесь как раз уместно ввести понятие чистой приведенной стоимости (ЧПС). Обозначая символом r учетную ставку для данной инвестиции, получаем следующую формулу NPV:
Где СFt
– денежное поступление от инвестиции в момент t; CF0 –поток средств (поступление) на текущий момент.Формула расчета в Excel чистой дисконтированной (приведенной) стоимости (NPV) = ЧПС(C1;B6:B10)+B5
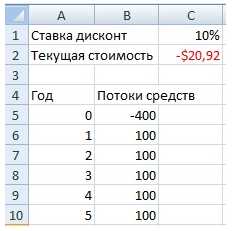
Терминология Excel, касающаяся дисконтируемых потоков денежных средств, несколько отличается от стандартной финансовой терминологии. В Excel сокращение МУР (ЧПС) обозначает приведенную стоимость (а не чистую приведенную стоимость) серии денежных поступлений.
Чтобы рассчитать в Excel чистую приведенную стоимость серии денежных поступлений в обычном понимании финансовой теории, необходимо сначала вычислить приведенную стоимость будущих денежных поступлений (с использованием такой функции Excel, как «ЧПС»), а затем вычесть из этого числа денежный поток на начальный момент времени. (Эта величина часто совпадает со стоимостью рассматриваемого актива.)
Автор: к.э.н. Жданов Иван Юрьевич
finzz.ru
Что такое чистая приведенная стоимость (NPV)?
Понятие «чистая приведенная стоимость» обычно всплывает в сознании, когда требуется оценить целесообразность тех или иных инвестиций.
Существуют математически обоснованные тезисы, в которых фигурирует концепция (чистой) приведенной стоимости и которых стоит придерживаться всякий раз, когда у вас возникает идея раскошелиться на тот или иной проект.
Чтобы понять, что такое чистая приведенная стоимость, мы детальнейшим образом разберем конкретный (гипотетический) пример.
Для этого нам придется вспомнить некоторые базовые сведения, относящиеся к теме приведенной стоимости, о которой в свое время мы уже вели речь на страницах сайта.
Итак, пример.
Чистая приведенная стоимость: вступление
Предположим, вам в наследство достался земельный участок стоимостью 23 тыс. долл. Плюс – на банковских счетах «завалялось» тысяч этак 280 «зеленых».
Итого – 303 тыс. долл., которые неплохо было бы куда-то пристроить.
На горизонте замаячил вариант со строительством инвестиционной недвижимости, цена на которую, как предполагают эксперты, через год должна резко устремиться ввысь.
Предположим, стоимость строительства некоего офисного здания составляет приемлемые для нас 280 тыс. долл., а предполагаемая цена продажи уже отстроенного здания – порядка 330 тыс. долл.
Если окажется, что приведенная стоимость 330 тыс. долл. окажется больше объема затраченных вами средств (280 000 долл. + 23 000 долл. = 303 000 долл.), то стоит соглашаться с предложением о строительстве объекта.
При этом разница между обеими величинами и будет той самой чистой приведенной стоимостью, к отысканию которой мы так стремимся.
Для начала, однако, нам придется разобраться с промежуточными расчетами, направленными на установление величины приведенной стоимости будущих доходов.
Как рассчитать приведенную стоимость
Очевидно, 330 тыс.долл., которые мы получим в будущем, стоят дешевле 330 тыс. долл., которыми мы располагаем сегодня. И дело не только в инфляции.
Основная причина такого положения вещей в том, что мы можем имеющиеся 330 тыс. долл. инвестировать в безрисковые финансовые инструменты наподобие банковских депозитов или государственных облигаций.
В таком случае для определения «истинной» стоимости наших 330 тыс. долл. к ним требуется присовокупить еще и процентный доход по соответствующему депозиту (ценной бумаге).
На эту ситуацию можно посмотреть так: сегодняшние 330 тыс. долл. будут стоит в будущем столько же плюс – процентный доход по безрисковым финансовым инструментам.
Мы вплотную приблизились к пониманию одного из важнейших принципов теории инвестирования: деньги СЕГОДНЯ стоят ДОРОЖЕ, чем деньги, которые мы получим ЗАВТРА.
Именно поэтому приведенная стоимость любого дохода в будущем будет МЕНЬШЕ его номинального значения, и чтобы его найти, нужно ожидаемый доход умножить на некоторый коэффициент, заведомо МЕНЬШИЙ единицы.
Обычно этот коэффициент именуется коэффициентом дисконтирования.
Математическая запись нашего постулата будет иметь следующий вид:
PV = DF * C1, где
PV – приведенная стоимость (от англ. present value),
DF – коэффициент (или – фактор) дисконтирования (от англ. discount factor),
C1 – ожидаемый через 1 год доход.
Сущность коэффициента дисконтирования может быть истолкована так: это нынешняя стоимость 1 доллара, который мы рассчитываем получить в будущем. Численно он будет равен следующему отношению:
DF = 1 / (1 + r), где
r – размер вознаграждения (норма доходности), на который вправе рассчитывать инвестор в связи с отсрочкой получения дохода.
Итак, мы готовы к тому, чтобы рассчитать, наконец, приведенную стоимость будущих доходов от наших инвестиций.
Для этого введем в условия задачи размер процентной ставки по безрисковым финансовым инструментам, равный, к примеру, 8 процентам годовых.
В таком случае ставка дисконтирования будет равняться значению дроби 1 / (1 + 0,08):
DF = 1 / (1 + 0,08) = 1 / 1,08 = 0,926.
Приведенную стоимость 330 тыс. долл. мы рассчитаем так:
PV = DF * C1 = 0,926 * 330 000 долл. = 305 580 долл.
Альтернативные издержки
Теперь вспомним, о чем мы вели речь в начале нашего разговора.
Если размер наших инвестиций окажется меньше приведенной стоимости того дохода, на который мы рассчитываем, значит соответствующее предложение является ВЫГОДНЫМ, и его следует принять.
Как видим, 303 000 долл. < 305 580 долл., а значит, строительство офиса на нашем участке (скорее всего) окажется выгодным вложением…
То, что только что проделали, на языке финансов звучит так: дисконтирование будущих доходов по ставке доходности, которую могут «предложить» иные (альтернативные) финансовые инструменты.
Обозначенную ставку доходности можно именовать по-разному: коэффициентом доходности, ставкой дисконтирования, предельной доходностью, альтернативными затратами на капитал, альтернативными издержками.
Все отмеченные варианты равноупотребимы, и их выбор зависит от контекста.
Стоит обратить внимание на термин «альтернативные издержки», поскольку он подчеркивает самую суть текущей стоимости денег, доходов и проч.
Именно из-за них теория финансов не рекомендует беспроцентно одалживать кому-нибудь деньги. Особенно на длительные сроки.
Вы просто будете нести ПОТЕРИ, равные альтернативным издержкам.
Ростовщики это отчетливо понимали тысячелетия назад, и потому предпочитали ссужать деньги не просто так, а под какой-никакой процент (тогда, заметьте, ни о какой инфляции никто даже не догадывался)…
Что такое «чистая приведенная стоимость»?
Итак, наше сооружение, которое мы планируем построить, обладает сегодняшней стоимостью в размере 305 580 долл.
Представим, что мы заделались-таки счастливыми обладателями этой суммы.
Что входит в эту сумму?
Разумеется, наши инвестиции в размере 303 000 долл. и еще какая-то часть, которая фактически образует некоторый (чистый) прирост стоимости.
Вот эту-то часть и принято именовать чистой приведенной стоимостью и обозначать литерным сочетанием NPV (от англ. net present value).
Расчет чистой приведенной стоимости (формула)
Итак, искомая формула расчета чистой приведенной стоимости (NPV) будет иметь следующий вид:
NPV = PV – C0 = C1 / (1 + r) – C0, где
С0 – величина инвестиций (оттока денежных средств) на сегодняшний момент.
Если NPV > 0, все «окей», инвестиции оправданны, смело бросаемся в бой.
Если NPV = 0, выбирайте вариант, наименее энергоемкий и наименее рисковый, так как итоговый результат вас мало утешит…
При NPV < 0 придется решительно отвергнуть предложение и продолжить поиски достойных объектов вложения.
На сегодня с теорией мы покончим.
Но впереди нас ждут не менее интересные публикации, позволяющие углубиться в тему чистой приведенной стоимости.
В конце концов, наша задача — подобраться к двум важнейшим принципам, на которых базируются верные инвестиционные решения.
Обо всем этом (и не только) – в другой раз.
Дополнительная информация по теме представлена в статьях:
1. Расчет NPV в Excel (пример),
2. Расчет NPV: онлайн-калькулятор.
Удачных инвестиций!
sprintinvest.ru
Приведенная стоимость: понятие и метод расчета
Под приведенной стоимостью понимают текущую стоимость денежных средств, которые будут получены в будущем. Приведенная стоимость – понятие, по своему значению противоположное будущей стоимости.
Если мы хотим узнать, сколько будут стоить наши инвестиции в будущем, нам придется воспользоваться концепцией будущей стоимости.
Если же мы хотим узнать, сколько денежные средства, которые мы получим в будущем, будут стоить сегодня, нам потребуется рассчитать соответствующие показатели с использованием концепции приведенной стоимости.
Приведенная стоимость: формулировка задачи
Понятие приведенной стоимости можно легко понять, попрактиковавшись на конкретных примерах.
Мы можем сформулировать в общем виде задачу, решением которой окажется рассматриваемое в настоящей статье понятие.
Наша задача будет иметь примерно такой вид: какую сумму денежных средств необходимо поместить на счет, по которому – с учетом капитализации на основе сложных процентов – начисляется n процентов, чтобы в будущем получить заранее определенную сумму денег.
В данном случае сумма денежных средств, которую мы поместим на счет сегодня, и будет являться приведенной стоимостью.
Значение n, являющееся процентной ставкой по вкладу, именуется ставкой дисконта (иногда эту величину именуют альтернативными издержками).
Важно: ставка дисконта – это ежегодная ставка доходности, на которую инвестор может рассчитывать на момент принятия инвестиционного решения.
Формула расчета приведенной стоимости
Рассмотрим простой пример. Допустим, что через год мы ожидаем получение дохода от инвестиций в размере 1000 долл.
При этом доступные нам финансовые инструменты предлагают максимальную доходность в размере 7% годовых.
Какую сумму денежных средств нам придется инвестировать, чтобы получить ожидаемый доход?
Иначе говоря, какова приведенная стоимость указанных денежных средств, дисконтированных по ставке 7%?

Рисунок 1. Внутри формулы расчета приведенной стоимости спрятан фактор дисконтирования
Для решения этой задачи составим простое уравнение, в котором обозначим приведенную стоимость как N. Тогда наше уравнение будет иметь вид:
N долл. * (1 + 0,07) = 1000 долл.
Решая уравнение, получим интересующее нас значение приведенной стоимости:
N долл. = 1000 долл. / (1 + 0,07) = 934,58 долл.
Полученный нами ответ означает, что сегодняшняя инвестиция в размере 934,58 долл. сроком на 1 год под 7% годовых обеспечит по истечении срока инвестирования получение дохода в размере 1000 долл.
Разумеется, приведенную стоимость можно рассчитывать и в случаях инвестирования средств на более длительный период.
Общая формула для этих случаев будет иметь следующий вид:
Nn = Sn / (1+k/100)n,
где Nn – приведенная стоимость, Sn – будущая стоимость денег в конце n-го периода, k – ставка дисконта (годовая процентная ставка), n – количество периодов инвестирования.
Например, приведенная стоимость 1000 долл., которые мы рассчитываем получить через три года в результате инвестирования, обеспечивающей доходность в размере 9% годовых, будет равна 772,18 долл.:
1000 долл. / (1 + 0,09)3 = 772,18 долл.
Таблица приведенной стоимости
Чем больше срок, для которого мы пытаемся рассчитать приведенную стоимость, тем сложнее становятся вычисления, связанные с возведением в степень дробных чисел.
Для упрощения процесса вычислений следует пользоваться уже упоминавшимися на страницах нашего сайта финансовыми таблицами либо вспомогательными вычислительными инструментами: калькуляторами, компьютерными программами.
В качестве примера приведу таблицу, содержащую факторы дисконтирования (приведения стоимости) для 1 долл.:
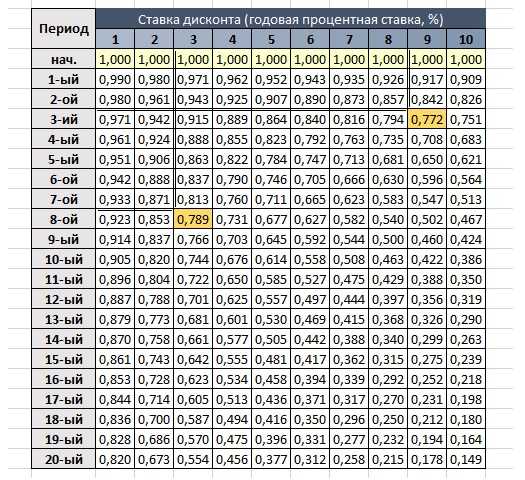
Рисунок 2. Таблица приведенной стоимости
Например, приведенная стоимость 1 долл., который предполагается получить через 3 года и который дисконтируется по ставке 9% годовых, равна 0,772 долл.
Это значение мы находим в таблице на пересечении столбца с индексом 9 и строки, соответствующей 3-ему периоду.
Чтобы узнать при тех же условиях приведенную стоимость 1000 долл., нужно 1000 долл. умножить на найденный нами фактор дисконтирования:
1000 долл. * 0,772 = 772 долл.
Полученное значение очень близко к ранее вычисленному нами точному значению – 772,18 долл.
Аналогично, приведенная стоимость 1 долл., дисконтируемого по ставке 3% годовых в течение восьми лет, равна, как следует из таблицы, 0,789 долл.
Отталкиваясь от этого значения, можно получить значения приведенной стоимости для любых сумм, дисконтируемых на тех же условиях.
Важные следствия
Анализируя нашу таблицу, можно сформулировать ряд важных следствий, связанных с понятием приведенной стоимости.
[1]. Фактор дисконтирования может быть равен 1 лишь в случае, когда ставка дисконта равна 0. Во всех остальных случаях он меньше 1.
[2]. С увеличением ставки дисконта (годовой процентной ставки) для конкретного года фактор дисконтирования уменьшается.
[3]. С увеличением срока, через который инвестор планирует получить конкретную сумму, размер приведенной стоимости (фактор дисконтирования) уменьшается.
Отмеченные особенности приведенной стоимости необходимо четко усвоить, поскольку эти знания пригодятся нам в будущем для математического обоснования целесообразности тех или иных инвестиций.
Дополнительная информация по теме представлена в статьях:
1. Расчет NPV в Excel (пример),
2. Расчет NPV: онлайн-калькулятор.
А на сегодня все. Удачных инвестиций!
sprintinvest.ru
Финансовый анализ и инвестиционная оценка предприятия
Оба понятия из заголовка этого раздела, дисконтированная (приведенная) стоимость, ПС (presentvalue, или PV), и чистая дисконтированная (приведенная) стоимость, ЧПС (netpresentvalue, или NPV), обозначают текущую стоимость ожидаемых в будущем денежных поступлений.
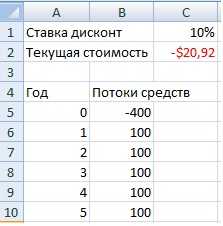
В качестве примера рассмотрим оценку инвестиции, обещающей доход 100 долл. в год в конце нынешнего и еще четырех следующих лет. Предполагаем, что эта серия из пяти платежей по 100 долл. каждый гарантирована и деньги непременно поступят. Если бы банк платил нам годовой процент в размере 10% при депозите на пять лет, то эти десять процентов как раз и составляли бы альтернативную стоимость инвестиции — эталонную норму прибыли, с которой мы сравнивали бы выгоду от нашего вложения.
Можно вычислить ценность инвестиции путем дисконтирования денежных поступлений от нее с использованием альтернативной стоимости в качестве ставки дисконтирования.
Формула расчета в Excel дисконтированной (приведенной) стоимости (PV) = ЧПС(C1;B5:B9)
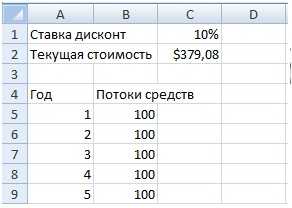
Приведенная стоимость (ПС) в объеме 379,08 долл. и есть текущая стоимость инвестиции.
Предположим, что данная инвестиция продавалась бы за 400 долл. Очевидно, она не стоила бы запрашиваемой цены, поскольку — при условии альтернативного дохода (учетной ставки) в размере 10% — реальная стоимость этого капиталовложения составляла бы только 379,08 долл. Здесь как раз уместно ввести понятие
Где СFt – денежное поступление от инвестиции в момент t; CF0 –поток средств (поступление) на текущий момент.
Формула расчета в Excel чистой дисконтированной (приведенной) стоимости (NPV) = ЧПС(C1;B6:B10)+B5
Терминология Excel, касающаяся дисконтируемых потоков денежных средств, несколько отличается от стандартной финансовой терминологии. В Excel сокращение МУР (ЧПС) обозначает приведенную стоимость (а не чистую приведенную стоимость) серии денежных поступлений.
Чтобы рассчитать в Excel чистую приведенную стоимость серии денежных поступлений в обычном понимании финансовой теории, необходимо сначала вычислить приведенную стоимость будущих денежных поступлений (с использованием такой функции Excel, как «ЧПС»), а затем вычесть из этого числа денежный поток на начальный момент времени. (Эта величина часто совпадает со стоимостью рассматриваемого актива.)
Автор: к.э.н. Жданов И.Ю.
Сайт: www.beintrend.ru
beintrend.ru
Чистая приведенная стоимость
Этот метод основан на сопоставлении величины исходной инвестиции с общей суммой дисконтированных чистых денежных поступлений, генерируемых ею в течение прогнозируемого срока. Поскольку приток денежных средств распределен во времени, он дисконтируется с помощью коэф-та r , устанавливаемого инвестором самостоятельно исходя из ежегодного % возврата, который он хочет или может иметь на инвестируемый им капитал.
Допустим, делается прогноз, что инвестиция будет генерировать в течение п лет, годовые доходы в размере Р1, Р2, …Рп.
Чистый приведенный эффект (NPV) – это разность между накопленной величиной дисконтированных доходов и суммой первоначальных инвестиций , т.е.
(NPV) = S — P
Очевидно, что если: NPV 0, то проект следует принять;
NPV 0, то проект следует отвергнуть;
NPV = 0, то проект ни прибыльной, ни убыточный.
Если по окончании периода реализации проекта планируется поступление средств в виде ликвидационной стоимости оборудования или высвобождения части оборотных средств, они должны быть учтены как доходы соответствующих периодов.
Расчет с помощью формул вручную достаточно трудоемок, поэтому для удобства применения этого и других методов, основанных на дисконтированных оценках, разработаны специальные статистические таблицы, в к-рых табулированы значения сложных %, дисконтирующих множителей, дисконтированного значения денежной единицы и т.п. в зависимости от временного интервала и значения коэф-та дисконтирования.
Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала пред-я в случае принятия рассматриваемого проекта. Этот показатель аддитивен во временном аспекте, т.е. NPV различных проектов можно суммирован. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.
Еще один инструмент дисконтирования денежных потоков – это внутренняя норма прибыли (или доходности) (ИРР = IRR), определяемая как ставка дисконтирования, при которой чистая приведенная стоимость = 0
Это собственная доходность проекта, если она выше стоимости капитала для фирмы, предложение приемлемо.
Значение показателя чистой приведенной стоимости для оценки эффективности инвестиций, порядок расчета
Используя метод диск-я, определяют стоимость, которую будет иметь инвестор через определенное число лет, и вычисляют сколько денег следует инвестировать сейчас для того, чтобы довести стоимость инвестиции до заданной (предполагаемой) величины при определенной ставке %.
Дисконтирование – это метод, применяемый при оценке и отборе инвестиционных программ.
Суть его заключается в приведении разновременных инвестиций и денежных поступлений к определенному периоду времени и определению К окупаемости капвлож. (внутренней нормы доходности — ВНД)
При выборе ставки дисконтирования необходимо ответить на вопрос: какая доходность на вложенные средства считается, с одной стороны, реальной, а с другой стороны – приемлемой для организации с учетом всех перечисленных выше обстоятельств.
Выбранную ставку называют ставкой ожидаемой доходности или ставкой альтернативного вложения средств.
Если ожидается, что проект будет ежегодно приносить денежные потоки, т.е. мы имеем дело с аннуитетом.
Кумулятивные коэф-ты дисконтирования или коэф-ты аннуитета, с их помощью исчисляют приведенную стоимость последовательности равных ежегодных платежей.
Чтобы получить чистую приведенную стоимость, необходимо дисконтировать денежные потоки, ожидаемые в связи с осуществлением инвестиционного проекта, по ставке, равной стоимости капитала для фирмы.
Когдадисконтированные денежные потоки превышают дисконтированные оттоки, ЧПС положительна – проект следует принять, а в противоположном случае НРУ отрицательна – проект следует отклонить.
Для облегчения расчета дисконтированной стоимости разработаны специальные таблицы.
На выбор дисконтной ставки влияет:
темп инфляции
банковские процентные ставки
ставки доходности иных альтернативных вложений
оценка рискованности инвестирования и т.д.
Одним из способов определения экономической целесообразности инвестиционного проекта является расчет ЧПС. Это дисконтированная стоимость, уменьшенная на сумму первоначальных инвестиционных затрат.
Если полученная т. о. величина будет положительной, то предложенный инвестиционный проект м. б. принят, если отрицательный = от проекта следует отказаться.
studfiles.net
NPV — метод чистой текущей стоимости
Область применения
NPV показывает чистые доходы или чистые убытки инвестора при помещении денег в проект по сравнению с хранением их в банке.
Описание
Величина NPV (Net Present Value) отражает чистую текущую стоимость и рассчитывается как разность между инвестициями и будущими доходами, выраженная в денежной величине, приведенной к началу реализации проекта, т. е. с учетом ставки дисконтирования.
Для определения NPV необходимо рассчитать текущую стоимость будущих оттоков и притоков денежных средств. При заданной норме дисконта её можно определить на протяжении всего жизненного цикла проекта, а также сопоставить приведенные суммы друг с другом.
Метод дисконтирования денежных поступлений – исследование денежного потока наоборот, т. е. от будущего к текущему моменту времени, позволяет привести будущие денежные поступления к сегодняшним условиям. Для этого используют формулу:
${PV_n}=\frac{CF_n}{(1+r)^n}={CF_n}*k_d$,
где $k_d$ — коэффициент дисконтирования,
$CF_n$ — доход от проекта за конкретный год,
$n$ — срок проекта в годах.
При начислении процентов несколько раз в году по сложной ставке применяется такая формула:
$${PV_n}=\frac{CF_n}{(1+\frac{r}{m})^{nm}}$$
Результатом сопоставления полученной величины и первоначальных инвестиций будет чистая текущая стоимость, которая показывает экономический результат реализации проекта.
$NPV=PV-CI$,
где $CI$ — сумма первоначальных инвестиций.
Если капитальные вложения, связанные с реализацией проекта, осуществляются в несколько этапов, то расчет показателя $NPV$ производится по следующей формуле:
$NPV = \sum \limits_{i=0}^{n} \frac{CF_i}{(1+r)^i} — \sum \limits_{i=0}^{n}\frac{CI_i}{(1+r)^i}$.
Интерпретация результатов:
- $NPV>0$ — проект является прибыльным и по окончании будет обеспечено получение прибыли согласно заданной ставке дисконта, а также будет получен дополнительный доход, равный величине $NPV$;
- $NPV=0$ — проект лишь окупает первоначальные затраты;
- $NPV
Важно: NPV показывает величину прибыли от инвестиции, и стоит предположить, что чем больше инвестиция, тем больше чистая текущая стоимость. Поэтому сравнение нескольких инвестиций разного размера с помощью этого показателя невозможно. Кроме того, величина NPV не несёт информации о периоде, через который инвестиция окупится.
При анализе проектов с различными исходными характеристиками (суммами первоначальных инвестиций, сроками экономической жизни и т. д.), кроме $NPV$, рассчитывают относительные показатели: индекс рентабельности и внутреннюю норму дохода.
Алгоритм
- Рассчитываем коэффициент дисконтирования ${k_d}=\frac{1}{(1+r)^n}$.
- Рассчитываем дисконтированные денежные поступлений $PV$.
- Рассчитываем дисконтированные денежные инвестиций $CI$.
- Рассчитать чистую текущую стоимость доходов $NPV$.

Требования к данным
| Имя поля | Метка поля | Тип данных | Вид данных |
|---|---|---|---|
| Year | Год | Целый | Непрерывный |
| Cash_flow | Денежные поступления | Вещественный | Непрерывный |
| Rate | Норма дисконта | Вещественный | Непрерывный |
| Investment | Инвестиции | Вещественный | Непрерывный |
| Project | Проект | Строковый | Дискретный |
Сценарий
basegroup.ru
Чистая приведенная стоимость (NPV). Расчет чистой приведенной стоимости :: BusinessMan.ru
Инвестиции будут оправданы лишь тогда, когда они способствуют созданию новых ценностей для владельца капитала. В этом случае определяется стоимость данных ценностей, превышающая расходы на их приобретение. Безусловно, возникает вопрос о том, можно ли оценить их больше реальной стоимости. Это доступно в том случае, если конечный результат более ценен в сравнении с суммарной ценой отдельных этапов, реализация которых позволила достичь этого результата. Для того чтобы понять это, следует узнать, что представляет собой чистая приведенная стоимость и как она рассчитывается.
Что такое приведенная стоимость?
Текущая или приведенная стоимость рассчитывается на базе концепции денег во времени. Она представляет собой показатель потенциала средств, направляемых на получение дохода. Она позволяет понять, сколько будет стоить в будущем сумма, которая доступна в настоящее время. Проведение соответствующего расчета имеет большое значение, так как платежи, которые совершены в различный период, могут поддаваться сравнению только после их приведения к одному временному отрезку.

Текущая стоимость образовывается в результате приведения к начальному периоду будущих поступлений и затрат средств. Она зависит от того, каким способом производится начисление процентов. Для этого используются простые или сложные проценты, а также аннуитет.
Что такое чистая приведенная стоимость?
Чистая приведенная стоимость NPV представляет собой разницу между рыночной ценой конкретного проекта и расходами на его реализацию. Аббревиатура, которая используется для ее обозначения, расшифровывается как Net Present Value.
Таким образом, понятие также можно определить как меру добавочной стоимости проекта, которая будет получена в результате его финансирования на начальном этапе. Главная задача состоит в том, чтобы реализовывать проекты, которые имеют положительный показатель чистой приведенной стоимости. Однако для начала следует научиться определять его, что поможет совершать наиболее выгодные инвестиции.
Основное правило NPV
Следует ознакомиться с основным правилом, которым обладает чистая приведенная стоимость инвестиций. Оно заключается в том, что величина показателя должна быть положительной для рассмотрения проекта. Его следует отклонить при получении отрицательного значения.

Стоит отметить, что рассчитываемая величина редко равна нулю. Однако при получении такого значения инвестору также желательно отвергнуть проект, так как он не будет иметь экономического смысла. Это обусловлено тем, что прибыль от вложения в дальнейшем не будет получена.
Точность расчета
В процессе расчета NPV стоит помнить о том, что ставка дисконтирования и прогнозы поступлений оказывают значительное влияние на текущую стоимость. В конечном результате могут быть погрешности. Это объясняется тем, что человек не может с абсолютной точностью сделать прогноз на получение прибыли в будущем. Следовательно, полученный показатель является только предположением. Он не застрахован от колебаний в разные стороны.
Безусловно, инвестору необходимо знать, какая прибыль будет им получена еще до вложения. Чтобы отклонения были минимальными, следует использовать наиболее точные методы для определения эффективности по совместительству с чистой приведенной стоимостью. Общее употребление различных методов позволит понять, будут ли выгодными вложения в определенный проект. Если инвестор уверен в правильности своих расчетов, можно принять решение, которое будет надежным.

Формула расчета
При поиске программ для определения чистой приведенной стоимости можно столкнуться с понятием «чистый дисконтированный доход», что имеет аналогичное определение. Рассчитать ее можно с помощью MS EXCEL, где она встречается под аббревиатурой ЧПС.
В применяемой формуле используются следующие данные:
- CFn – денежная сумма за период n;
- N – количество периодов;
- i – ставка дисконтирования, которая вычисляется из годовой процентной ставки
Кроме того, денежный поток за определенный период может быть нулевым, что эквивалентно его полному отсутствию. При определении дохода денежная сумма записывается со знаком «+», для расходов — со знаком «-«.

В итоге расчет чистой приведенной стоимости приводит к возможности оценки эффективности вложений. Если NPV>0, инвестиция окупится.
Ограничения в применении
Пытаясь определить, какой будет чистая приведенная стоимость NPV, с помощью предложенной методики, следует обратить внимание на некоторые условия и ограничения.
В первую очередь принимается предположение, которое состоит в том, что показатели инвестиционного проекта на протяжении его реализации будут стабильными. Однако вероятность этого может приблизиться к нулю, так как большое количество факторов влияет на величину денежных потоков. Спустя определенное время может измениться стоимость капитала, направленного на финансирование. Следует отметить, что в будущем полученные показатели могут значительно измениться.
Не менее важным моментом является выбор ставки дисконтирования. В качестве нее можно применить стоимость капитала, привлекаемого для инвестирования. С учетом фактора риска ставка дисконтирования может корректироваться. К ней прибавляется надбавка, поэтому чистая приведенная стоимость уменьшается. Подобная практика не всегда является оправданной.

Использование надбавки за риск означает, что инвестором в первую очередь рассматривается только получение убытка. Он по ошибке может отклонить прибыльный проект. Ставкой дисконтирования также может выступать доходность от альтернативных инвестиций. К примеру, если капитал, применяемый для инвестирования, будет вложен в другое дело со ставкой в 9%, ее можно принять за ставку дисконтирования.
Преимущества использования методики
Расчет чистой текущей стоимости имеет следующие преимущества:
- показатель учитывает коэффициент дисконтирования;
- при принятии решения используются четкие критерии;
- возможность использования при расчете рисков проекта.
Однако стоит учитывать, что данный метод имеет не только достоинства.
Недостатки использования методики
Чистая приведенная стоимость инвестиционного проекта обладает следующими отрицательными качествами:
- В некоторых ситуациях довольно проблематично выполнить корректный расчет ставки дисконтирования. Это чаще всего касается многопрофильных проектов.
- Несмотря на то, что денежные потоки прогнозируются, с помощью формулы невозможно рассчитать вероятность исхода события. Применяемый коэффициент может учитывать инфляцию, но в основном ею выступает норма прибыли, закладываемая в расчетный проект.

После подробного ознакомления с понятием «чистая приведенная стоимость» и порядком расчета, инвестор может сделать вывод о том, стоит ли использовать рассматриваемую методику. Для определения эффективности вложений ее желательно дополнить другими похожими способами, что позволит получить наиболее точный результат. Однако нет абсолютной вероятности, что он будет соответствовать действительному получению прибыли или убытка.
businessman.ru
